付録: AI はどのように文章を生成するか?
ここでは面倒な理論を全部すっ飛ばして感覚で理解してみましょう! "自然言語"で説明することが難しくても、我々にはプログラミング言語があります!ここでは JavaScript を使って大まかな雰囲気を理解していくことにしましょう。
※ 普通 Deep Learning といえば Python なのですが、N予備校プログラミングコースアドベントカレンダー、ということでおそらく多くの人が触れるであろう JavaScript で説明をします。
※ 雰囲気で理解するために JavaScript の文法で書いています。掲載している JavaScript のコードを動かすことはできません。
注意
ここでは分かりやすさのために自然言語生成としてのAIの話をしています。 コードの自動生成ではありません。ですが、コードを自然言語としてみなせば同じ話が適用できるのであまり気にしないでください。
注意2
雰囲気を理解するために厳密性をすっ飛ばして書いています。
興味を持った方はぜひしっかりとした書籍や講座などを見て正しい知識を手に入れてください!
このページは画像生成AIのときにあった「絵師の画像をつぎはぎ加工でコラージュして絵を作ってるんだ!」 みたいな悲しい誤解を生みたくなくて書いています。(あの問題はデータセットが良くないとかが本質だと思っているので)
TL;DR
- 文章生成AIは (基本的には) 次単語を予測する関数である
- 次単語を予測する関数を繰り返し適用することで文章を生成できる
- 次単語を予測する関数はニューラルネットワークで作れる
- 文章生成AIの根幹部分であるモデルは次単語の確率分布を出力する
文章生成 AI は"次単語予測関数"だ!
いきなりですが文章生成 AI の正体は「次の単語を予測する関数」です。 この説明だけだと分かりづらいので JavaScript のコードに落としてしまいましょう。 例えば次の処理なんてどうでしょう?
function selectNextWord(text) {
// なんらかの強そうな処理
return nextWord;
}
const prompt = "今日は良い";
const predicted = selectNextWord(prompt);
console.log(predicted) // => "天気"
console.log(prompt + predicted); // => "今日は良い天気"プロンプト (入力) として「今日は良い」を与えると、次単語予測関数 selectNextWord は「天気」を出力します。
したがってこのプログラムの出力は「今日は良い天気」となります。
これだと長い文章は生成できないので、どんどん伸ばしていきましょう。
let generatedText = "今日は良い";
let predictedWord = "";
while (nextWord !== "[EOS]") {
predictedWord = selectNextWord(generatedText);
generatedText += predictedWord;
}
console.log(generatedText);
// => "今日は良い天気ですね。[EOS]"このプログラムでは生成された文 generatedText に予測された次単語 predictedWord を無限に連結させています。
ただし、予測された単語が [EOS] であった場合はループを抜けます。[EOS] は End of sequence の略で「単語列の終端」を表します。</s> と表されることもあります。
今回の場合は
| ループ | 入力した文 | 予測された単語 | 生成された文 |
|---|---|---|---|
1 | 今日は良い | 天気 | 今日は良い天気 |
2 | 今日は良い天気 | です | 今日は良い天気です |
3 | 今日は良い天気です | ね | 今日は良い天気ですね |
4 | 今日は良い天気ですね | 。 | 今日は良い天気ですね。 |
5 | 今日は良い天気ですね。 | [EOS] | 今日は良い天気ですね。[EOS] |
となります。
ならば selectNextWord は何を……?
ここまでで意味が分からなかった点が一つあります。それは selectNextWord はどんな魔法で動いているのか? ということです。 ここで新たな魔法 モデル と トークナイザ を使って selectNextWord を書いていきましょう。
function selectNextWord(text) {
const tokenized = tokenizer(text);
const logits = model(tokenized);
const finalWordLogits = logits.slice(-1)[0];
let maxIdx = 0;
for (const i in finalWordLogits) { // i = 0, 1, 2, ...
if (finalWordLogits[maxIdx] < finalWordLogits[i]) {
maxIdx = i;
}
}
return tokenizer.decode(maxIdx);
}トークナイザとは?
トークナイザ はテキストを「単語列」に切り分け、それぞれの単語を数字に置き換える役割をする関数です。 もしかしたら国語の授業で「分かち書き」ということをしたことがあるかもしれません。トークナイザはそれをします。
さらにトークナイザは生成した単語列から整数列を作ります。例えばトークナイザが次のような辞書を持っているとしましょう。
| index | 単語 | 備考 |
|---|---|---|
| 0 | [BOS] | 文章の開始 |
| 1 | [EOS] | 文章の終了 |
| 2 | [UNK] | 未知の単語 |
| 3 | 。 | |
| 4 | 良い | |
| 5 | 天気 | |
| 6 | は | |
| 7 | 今日 | |
| 8 | です |
この場合、トークナイザは
"今日は良い天気です。"
=> "今日" / "は" / "良い" / "天気" / "です" / "。"
=> [7, 6, 4, 5, 8, 3]と文章を分解し、整数列に変換します。実際の文章生成 AI はこの辞書がもっと大きいです。 例えば rinna 社のトレーニングした日本語 GPT-2 モデルは 44876 もの単語を持っています。
ならばモデルは何を……?
まずモデルがやっていることをここで説明することは難しいです。詳しく知りたい方は書籍等を見てみてください。 ここでは簡単にふわっと雰囲気を説明します。
まず一文で言えば「モデルには学習可能なパラメータが含まれており、そのパラメータと入力でうまいこと計算をして出力を決定する」です。
学習可能なパラメータとは?
ベクトルの微分により決定される値です。始めは ランダムな値 を振りますが、ベクトルの微分により決定される値で少しずつ改善していくことで、解きたい問題に合ったパラメータに変化していきます。
例えば から を求める関数をニューラルネットワークで作ってみましょう。(x * x すれば良いと言われればそうですけど!)
あまりにも突然ですが次のような式を考えてみます。
これは Linear(1, 3), ReLU, Linear(3, 1) というネットワークを式にしたものです(ここは理解しなくて良いです)。またこれも理解しなくて良いですが、ReLU は という関数です。
学習のためにデータセットを準備します。 x = (1.01, 1.02, 1.03, ..., 99.99, 100.00) からランダムに 8000 個取り出し、x_train とします。そして x_train のそれぞれの値を2乗したものを y_train とします。この x_train と y_train を使ってニューラルネットワークを学習させましょう。
が になるように、 をうまく"トレーニング"していきます。パラメータの数は 10 個ありますから、10 次元空間を探索して と がうまく重なるような点を探せば良いです。
以下のコードを使って学習させます。(コードは読まなくて良いです。)
学習コード (あまり綺麗ではないです)
import torch
import matplotlib.pyplot as plt
import numpy as np
from torch import nn
from tqdm import tqdm
# モデルの定義
class MyModel(nn.Sequential):
def __init__(self):
super().__init__(
nn.Linear(1, 3),
nn.ReLU(),
nn.Linear(3, 1),
)
# 学習するパラメータの出力
def print_params(model: MyModel):
p = []
p_label = [
'a1', 'a2', 'a3', 'b1', 'b2', 'b3',
'a4', 'a5', 'a6', 'b4'
]
for params in model.parameters():
for para in params.flatten():
p.append(para.item())
for para, label in zip(p, p_label):
print(f'{label}: {para:.3e}', end=', ')
print()
# 学習
def train():
torch.manual_seed(42)
x_axis = np.arange(1, 100, 0.01)
# データセットの準備
x_axis_shuffled = np.random.permutation(x_axis)
y_axis_shuffled = x_axis_shuffled * x_axis_shuffled
x_train, x_test = x_axis_shuffled[:8000], x_axis_shuffled[8000:]
y_train, y_test = y_axis_shuffled[:8000], y_axis_shuffled[8000:]
x_dataset = torch.from_numpy(x_train).float()
y_dataset = torch.from_numpy(y_train).float()
# モデルの準備
model = MyModel()
# パラメータの初期値の出力
print_params(model)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
criterion = nn.MSELoss()
num_epochs = 10
losses = []
for epoch in tqdm(range(num_epochs)):
losses_each_epoch = []
# 1 epoch 分の学習
model.train()
for x, y in zip(x_dataset, y_dataset):
out = model(x.unsqueeze(0))
loss = criterion(out, y.unsqueeze(0))
losses_each_epoch.append(loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 1 epoch 分の検証
model.eval()
with torch.no_grad():
y_pred = model(torch.from_numpy(x_test).float().unsqueeze(0).T)
y_pred = y_pred.numpy().flatten()
s_x_test, s_y_test, s_y_pred = zip(*sorted(zip(x_test, y_test, y_pred)))
plt.plot(s_x_test, s_y_pred, 'c-',
label=f'prediction (epoch {epoch + 1})',
alpha=(epoch + 1) / num_epochs)
if epoch == num_epochs - 1:
plt.plot(s_x_test, s_y_test, 'm-', label='ground truth')
print_params(model)
losses.append(np.mean(losses_each_epoch))
plt.legend()
plt.show()
# Epoch ごとの Loss の出力
plt.plot(range(num_epochs), losses, label='loss')
plt.show()
# 結果の表示
model.eval()
with torch.no_grad():
y_pred = model(torch.from_numpy(x_test).float().unsqueeze(0).T)
y_pred = y_pred.numpy().flatten()
# sort x_test and y_test and y_pred
x_test, y_test, y_pred = zip(*sorted(zip(x_test, y_test, y_pred)))
print(list(zip(x_test, y_pred)))
plt.plot(x_test, y_pred, label='prediction')
plt.plot(x_test, y_test, label='ground truth')
plt.legend()
plt.show()
if __name__ == '__main__':
train()ここで パラメータの変化 を追いかけていきます。 縦を見ていくとそれぞれのパラメータが徐々に変化していくことが分かります。
[initial] a1: 7.645e-01, a2: 8.300e-01, a3: -2.343e-01, b1: 9.186e-01, b2: -2.191e-01, b3: 2.018e-01, a4: -2.811e-01, a5: 3.391e-01, a6: 5.090e-01, b4: -4.236e-01,
[epoch 1] a1: 6.548e+00, a2: 6.514e+00, a3: -2.343e-01, b1: -1.892e+01, b2: -1.985e+01, b3: 2.018e-01, a4: 5.892e+00, a5: 6.098e+00, a6: 5.090e-01, b4: -1.928e+01,
[epoch 2] a1: 5.810e+00, a2: 5.777e+00, a3: -2.343e-01, b1: -4.590e+01, b2: -4.686e+01, b3: 2.018e-01, a4: 7.261e+00, a5: 7.543e+00, a6: 5.090e-01, b4: -4.541e+01,
[epoch 3] a1: 4.803e+00, a2: 4.763e+00, a3: -2.343e-01, b1: -6.887e+01, b2: -6.988e+01, b3: 2.018e-01, a4: 9.934e+00, a5: 1.032e+01, a6: 5.090e-01, b4: -6.634e+01,
[epoch 4] a1: 4.096e+00, a2: 3.960e+00, a3: -2.343e-01, b1: -8.500e+01, b2: -8.641e+01, b3: 2.018e-01, a4: 1.348e+01, a5: 1.402e+01, a6: 5.090e-01, b4: -7.723e+01,
[epoch 5] a1: 4.420e+00, a2: 2.857e+00, a3: -2.343e-01, b1: -9.158e+01, b2: -9.759e+01, b3: 2.018e-01, a4: 1.631e+01, a5: 1.751e+01, a6: 5.090e-01, b4: -7.404e+01,
[epoch 6] a1: 4.848e+00, a2: 2.008e+00, a3: -2.343e-01, b1: -9.463e+01, b2: -1.073e+02, b3: 2.018e-01, a4: 1.780e+01, a5: 2.537e+01, a6: 5.090e-01, b4: -6.693e+01,
[epoch 7] a1: 4.871e+00, a2: 1.913e+00, a3: -2.343e-01, b1: -9.400e+01, b2: -1.129e+02, b3: 2.018e-01, a4: 1.753e+01, a5: 3.346e+01, a6: 5.090e-01, b4: -5.220e+01,
[epoch 8] a1: 4.958e+00, a2: 1.922e+00, a3: -2.343e-01, b1: -9.120e+01, b2: -1.157e+02, b3: 2.018e-01, a4: 1.655e+01, a5: 3.823e+01, a6: 5.090e-01, b4: -3.459e+01,
[epoch 9] a1: 5.034e+00, a2: 1.945e+00, a3: -2.343e-01, b1: -8.902e+01, b2: -1.168e+02, b3: 2.018e-01, a4: 1.577e+01, a5: 4.008e+01, a6: 5.090e-01, b4: -1.901e+01,
[epoch 10] a1: 5.066e+00, a2: 1.968e+00, a3: -2.343e-01, b1: -8.785e+01, b2: -1.172e+02, b3: 2.018e-01, a4: 1.533e+01, a5: 4.061e+01, a6: 5.090e-01, b4: -5.998e+00,そして最終的にはこのように推論できました。
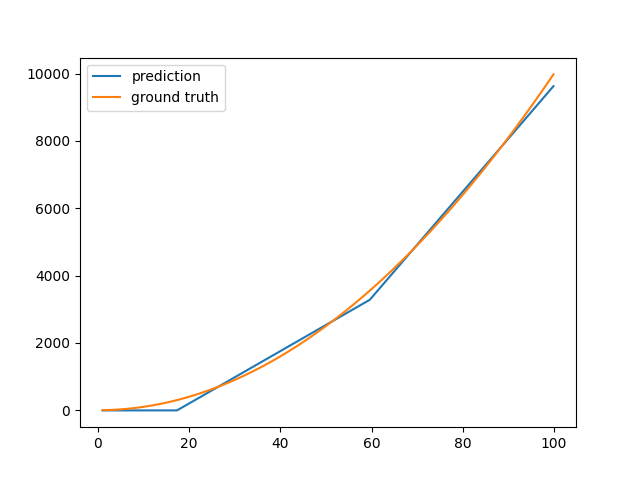
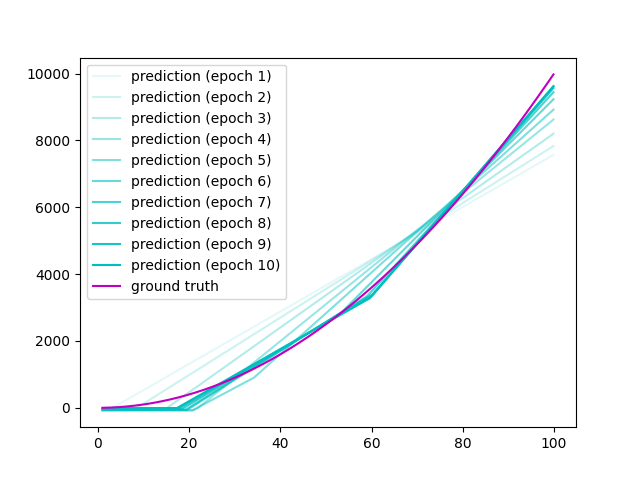
このように徐々にパラメータを変化させ、正解に近づけることをパラメータの学習と言います。なので、学習されるパラメータ はそれぞれを徐々に変化させることによって勝手に決まるものなんだな〜と思ってください。
???
よく分かりませんね。
さて、文章はトークナイザにより整数列に変換されるのでした。
"今日は良い天気です。"
=> "今日" / "は" / "良い" / "天気" / "です" / "。"
=> [7, 6, 4, 5, 8, 3]次にこれらを Embedding 層 と呼ばれるものを使って単語埋め込みと呼ばれるベクトルへ変換します。
[7, 6, 4, 5, 8, 3]
=> [
[-0.6116, -2.1513, 1.0583, 0.2867], // 7 番の単語埋め込み
[-1.0342, -1.4701, 0.4346, 0.1900], // 6 番の単語埋め込み
[-1.3626, -2.1539, -0.0992, 0.4266], // 4 番の単語埋め込み
[ 1.1974, 0.9273, -1.1307, 0.0282], // 5 番の単語埋め込み
[-1.2594, 0.7299, 1.1717, 0.7349], // 8 番の単語埋め込み
[ 0.3922, -0.9334, -0.1587, 0.2792], // 3 番の単語埋め込み
]単語埋め込みとして有名なものに word2vec というものがあります。 東京 - 日本 + アメリカ = ワシントン D.C. みたいなやつです。
この単語埋め込みも 学習可能なパラメータ です。つまり初期値はランダムで、学習の過程でそれらしくなっていきます。
次にこの単語埋め込みからなる行列に対して、行列 (学習可能) で掛け算して、非線形な関数に通して、また次の行列 (学習可能) で掛け算して……を繰り返します。
補足
本当は、テキストの処理は RNN とか Transformer とかを使うのであって、
直接埋め込みベクトルからなる行列に行列を掛け算するわけではないです。
これを説明すると大変なのでだいぶ雑に書いています。要するに嘘なので、気になる人にはやっぱり本を読んでほしいです。
(なぜ嘘なのかというと、単純に行列をかけるだけでは単語間の関係を捉えることができないからです。これは行列演算についてよく考えてみると分かります)
(でも flatten して固定長のネットワークにすればできなくもないかもしれません?どうなんですかね)
そして最終的に次単語を選ぶため、[語彙数]次元 のベクトルに変換します。
[7, 6, 4, 5, 8, 3]
// Embedding
=> [
[-0.6116, -2.1513, 1.0583, 0.2867], // 7 番の単語埋め込み
[-1.0342, -1.4701, 0.4346, 0.1900], // 6 番の単語埋め込み
[-1.3626, -2.1539, -0.0992, 0.4266], // 4 番の単語埋め込み
[ 1.1974, 0.9273, -1.1307, 0.0282], // 5 番の単語埋め込み
[-1.2594, 0.7299, 1.1717, 0.7349], // 8 番の単語埋め込み
[ 0.3922, -0.9334, -0.1587, 0.2792], // 3 番の単語埋め込み
]
なんらかの演算
=> [-0.4579, -0.9935, 0.4670, 1.0983, -1.3966, 0.6078, 0.7137, 1.2820, -0.1386]得られた出力を、softmax 関数と呼ばれる関数に通します。
JavaScript で書いたときのイメージ
// 配列内の合計を計算
function sum(arr) {
return arr.reduce((a, b) => a + b, 0);
}
function softmax(x_vector) {
const expSum = sum(x_vector.map(x => Math.exp(x)));
return x_vector.map(x => Math.exp(x) / expSum);
}注意
これはイメージとしてのコードであり、 実際にこれをそのまま使って計算すると計算結果が爆発する可能性があります (指数関数なので)。 実際にはもう少し工夫した実装をします。(あと分母に eps とか足したいですよね)
softmax は
- ベクトルの各要素を 0 以上 1 以下にする
- ベクトルの要素の合計をちょうど 1 にする
という効果があるので は確率分布とみなすことができます。
つまり、モデルは入力された整数列を確率分布に変換します。 確率分布は次にくる単語の出現確率のようなものに対応する (ように学習させる) ので、
- この確率分布に従うようにサンプリング
- 確率最大の単語を選択する
などをすれば、良さそうな次単語を選択できるようになります。
このように学習させるためには大量の文章をモデルに流し、 「出力により得られた次単語」と「実際の次単語」の誤差を減らすようにすれば良いです。
まとめ
以上のようにして文章生成 AI は文章を生成しています。TL;DR を再掲しておきます。
- 文章生成AIは (基本的には) 次単語を予測する関数である
- 次単語を予測する関数を繰り返し適用することで文章を生成できる
- 次単語を予測する関数はニューラルネットワークで作れる
- 文章生成AIの根幹部分であるモデルは次単語の確率分布を出力する
実際にはもっと複雑なアーキテクチャを使っていたり、もっと複雑なサンプリングをしていたり、もっと複雑な微調整をしていたりします。 興味を持った方はぜひ本編で紹介した本や講座などを覗いてみてください!