つまみログ

ある点Pから最も近い半直線上の点Qを計算する

証明とProcessingによるビジュアライズ

投稿日
読了予想時間
7 分
tag emoji技術
tag emoji数学

こんにちは、つまみ (@TrpFrog) です。生まれてから一度も歩いたことがありません。

大学の課題でタイトルの内容をどうしても計算したくなる機会があったのですが僕のググり力不足かヒットせず、 泣く泣く自力で計算する羽目になったので覚書を残します。 数学的な議論が怪しいのはご容赦ください。(は？)(ツッコミがあればお願いします)

あとProcessing.jsを使ってみよう！ ということで、記事の最後に触って確かめられるProcessingのコードを載せました。

前提知識

この記事における前提知識は

  • 三角関数 (sin⁡,cos⁡,tan⁡,arctan)\sin, \cos, \tan, \mathrm{arc\hspace{0px}tan})
  • 高校数学レベルのベクトル
  • 行列の積と回転行列

です。結果を知りたいだけならばこの知識は不要です。

解きたい問題

次のような問題が解きたいです。

問題

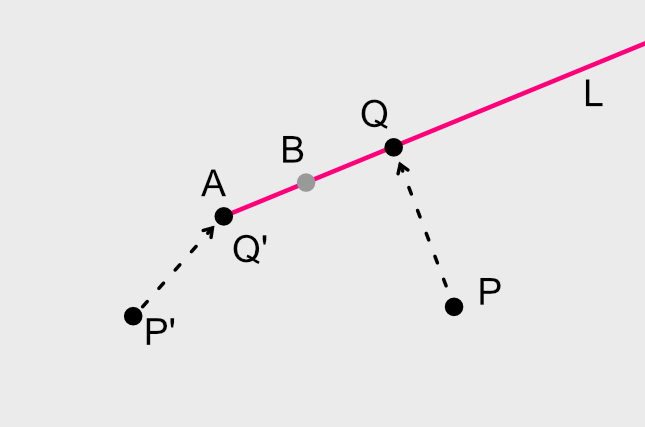
xyxy 平面上に点 AA から点 BB 方向に伸びる半直線 LL と、点 PP があります。 このとき、点 PP から最も近い LL 上の点 QQ を求めてください。

![](/blog/half-line/thumbnail?w=645&h=427)

直線で考える

さて、いきなり半直線で考えるのは大変そうなので直線で考えてみましょう。すると次のような問題になります。

問題 (2)

xyxy 平面上に直線 ABAB と点 P(x,y)P(x, y) があります。 このとき、点 PP から最も近い直線 ABAB 上の点 RR を求めてください。

この問題は簡単です。直線 ABAB に向けて点 PP から下ろした垂線とその交点が RR となります。さてそのような RR を実際に求めてみましょう。

ベクトル方程式で表す

原点を OO としたとき, a⃗=OA→,b⃗=OB→,v⃗=AB→\vec{a} = \overrightarrow{OA}, \vec{b} = \overrightarrow{OB}, \vec{v} = \overrightarrow{AB} とします。また、直線 ABAB 上の点 RR の位置ベクトルを r⃗\vec r とします。このとき直線 ABAB のベクトル方程式はパラメータ tt を用いて次のように表すことができます。

r⃗=a⃗+tv⃗(1)\vec r = \vec a + t \vec v \tag{1}

また、v⃗\vec v の同じ大きさの法線ベクトルを u⃗\vec u とします。すなわち

v⃗⋅u⃗=0,∣v⃗∣=∣u⃗∣\vec v \cdot \vec u = 0, \quad |\vec v| = |\vec u|

となるようなベクトル u⃗\vec u です。このとき、平面上の任意の点 PP の位置ベクトル p⃗\vec p はパラメータ s,ts, t を用いて次の式で表すことができます。

p⃗=a⃗+sv⃗+tu⃗(2)\vec p = \vec a + s \vec v + t \vec u \tag{2}

これらの情報から点 RR を求めてみます。RR は直線 ABAB に向けた垂線と直線の交点でした。u⃗\vec u と v⃗\vec v は直交しますから、求める点 RR の位置ベクトル r⃗\vec r は式 (2) におけるパラメータをそのまま使って次のように表すことができます。

r⃗=a⃗+sv⃗(3)\vec r = \vec a + s \vec v \tag{3}

これで問題(2) の答えがわかりました！ めでたしめでたし……ではなく s,ts, t を求める必要があります。

Pの座標からパラメータを求める

式(2) を変形して次のような式を作ります。

p⃗−a⃗=sv⃗+tu⃗\vec p - \vec a = s \vec v + t \vec u

u⃗\vec u と v⃗\vec v は直行していますから、p⃗−a⃗\vec p - \vec a を v⃗\vec v が xx 軸と平行になるように回転してあげて、そのときの xx 座標を ∣v⃗∣|\vec v| で割った値を読むと uu がわかります。これは v⃗\vec v の xx 軸となす角 (反時計回りを正とする) を θ\theta として次のように表すことができます。

[st]=1∣v⃗∣[cos⁡(−θ)−sin⁡(−θ)sin⁡(−θ)cos⁡(−θ)][x−xAy−yA]=1∣v⃗∣[cos⁡θsin⁡θ−sin⁡θcos⁡θ][x−xAy−yA]=1∣v⃗∣[(x−xA)cos⁡θ+(y−yA)sin⁡θ−(x−xA)sin⁡θ+(y−yAcos⁡θ]\begin{align*} \begin{bmatrix} s \\ t \end{bmatrix} &= \frac{1}{|\vec v|} \begin{bmatrix} \cos(-\theta) & -\sin(-\theta) \\ \sin(-\theta) & \cos(-\theta) \end{bmatrix} \begin{bmatrix} x - x_A \\ y - y_A \end{bmatrix}\\ &= \frac{1}{|\vec v|} \begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} x - x_A \\ y - y_A \end{bmatrix}\\ &= \frac{1}{|\vec v|} \begin{bmatrix} (x - x_A)\cos\theta + (y - y_A)\sin\theta \\ -(x - x_A)\sin\theta + (y - y_A\cos\theta \end{bmatrix} \end{align*}

従って RR を求めるのに必要だったパラメータ ss は

s=(x−xA)cos⁡θ+(y−yA)sin⁡θ∣v⃗∣s = \frac{(x - x_A) \cos \theta + (y - y_A) \sin \theta}{|\vec v|}

であるとわかりました。

v⃗\vec v の xx 軸となす角 θ\theta を求める

次に ss を求めるのに必要な θ\theta を計算しましょう。v⃗=AB→=b⃗−a⃗\vec v = \overrightarrow{AB} = \vec b - \vec a であったことを思い出してください。つまり直線 ABAB の傾きが求まれば良いです。ここで A(xA,yA),B(xB,yB)A(x_A, y_A), B(x_B, y_B) とすると

tan⁡θ=yB−yAxB−xAθ=arctanyB−yAxB−xA\begin{align*} \tan \theta &= \frac{y_B -y_A}{x_B-x_A}\\ \theta &= \mathrm{arc\hspace{0px}tan}\frac{y_B -y_A}{x_B-x_A} \end{align*}

です。ただし xB−xA≠0x_B - x_A \neq 0 。xB−xA=0x_B - x_A = 0 の時は今回は議論しません。ここについては各プログラミング言語の標準ライブラリとして存在するはずの便利関数 atan2(y,x)\mathrm{atan\hspace{0px}2}(y, x) を用いて

θ=atan2(yB−yA,xB−xA)\theta = \mathrm{atan\hspace{0px}2}(y_B -y_A, x_B-x_A)

を使ってください。(は？)

以上の議論より、問題(2)の答えの点 RR の位置ベクトル r⃗\vec r は

r⃗=a⃗+sv⃗s=(x−xA)cos⁡θ+(y−yA)sin⁡θ∣v⃗∣θ=atan2(yB−yA,xB−xA)\begin{align*} \vec r &= \vec a + s\vec v\\ s &= \frac{(x - x_A) \cos \theta + (y - y_A) \sin \theta}{|\vec v|}\\ \theta &= \mathrm{atan\hspace{0px}2}(y_B -y_A, x_B-x_A) \end{align*}

であると分かりました。

半直線の問題を解く

さて、ここまでで元の問題の9割は解き終わりました。ここで元の問題についてもう一度考えてみましょう。

問題

xyxy 平面上に点 AA から点 BB 方向に伸びる半直線 LL と、点 PP があります。 このとき、点 PP から最も近い LL 上の点 QQ を求めてください。

結論から述べると、点 QQ の位置ベクトルを q⃗\vec q としてこの問題の答えは次の通りです。

q⃗=a⃗+max⁡(0,s)v⃗a⃗=(xA,yA)b⃗=(xB,yB)v⃗=b⃗−a⃗s=(x−xA)cos⁡θ+(y−yA)sin⁡θ∣v⃗∣θ=atan2(yB−yA,xB−xA)\begin{align*} \vec q &= \vec a + \max(0, s)\vec v\\ \vec a &= (x_A, y_A) \\ \vec b &= (x_B, y_B ) \\ \vec v &= \vec b - \vec a\\ s &= \frac{(x - x_A) \cos \theta + (y - y_A) \sin \theta}{|\vec v|}\\ \theta &= \mathrm{atan\hspace{0px}2}(y_B -y_A, x_B-x_A) \end{align*}

v⃗\vec v の係数を max⁡(0,s)\max(0, s) としただけです。なぜこうなるかは簡単です。パラメータ ss は直線のときと同様の議論をすることで

r⃗=a⃗+sv⃗\vec r = \vec a + s \vec v

を満たすような ss であることがわかります。このとき半直線 ABAB に乗らないように、RR を点 AA から点 BB と反対方向に動かしていくと s<0s < 0 となってしまいます。よって負の数だけをカットすれば良く、v⃗\vec v の係数は max⁡(0,s)\max(0, s) であるとわかります。

本当にそうなるの？

数学が下手くそな人間が数字をこねくり回してるだけでは信憑性に欠けるので(？)確認用のProcessingのコードを置いておきます。また、下の画像をマウスオーバーすることでそのような点 QQ が描画されます。実際に上で示した式が正しいことを動かして確認してみてください。

Java
PVector A, B;

void halfStraightLine(float x1, float y1, float x2, float y2) {
    final int INF = 10000;
    line(x1, y1, x1 + (x2 - x1) * INF, y1 + (y2 - y1) * INF);
}

PVector calcQ(float x, float y) {
    float theta = atan2(B.y - A.y, B.x - A.x);
    float d = dist(A.x, A.y, B.x, B.y);
    float s = (cos(theta) * (x - A.x) + sin(theta) * (y - A.y)) / d;
    x = A.x + Math.max(0, s) * (B.x - A.x);
    y = A.y + Math.max(0, s) * (B.y - A.y);
    return new PVector(x, y);
}

void setup() {
    size(300, 400);
    A = new PVector(100, 100);
    B = new PVector(200, 300);
}

void draw() {
    background(245);

    stroke(0);
    halfStraightLine(A.x, A.y, B.x, B.y);
    noStroke();

    final PVector p = new PVector(mouseX, mouseY);
    final PVector q = calcQ(p.x, p.y);
    final int r = 10;

    textSize(16);
    fill(200);
    text("A", A.x + r, A.y + r);
    text("B", B.x + r, B.y + r);
    ellipse(A.x, A.y, r, r);
    ellipse(B.x, B.y, r, r);

    fill(0);
    text("P", p.x + r, p.y + r);
    text("Q", q.x + r, q.y + r);

    fill(#dbbb92);
    ellipse(p.x, p.y, r, r);

    fill(#90e200);
    ellipse(q.x, q.y, r, r);
}
記事一覧ツイート訂正リクエスト